pycrtools.tasks.pulsecal

Axes3D(fig[, rect])	3D axes object.
DirectionFitTriangles([ws, parfile])	Find the direction of a source provided one has the measured delay of arrival and the positions of the antenna.
FitMaxima([ws, parfile])	Find the maxima in multiple datsets and fit a basis spline polynomial to the data around their respective maximum.
LocatePulseTrain([ws, parfile])	Usage
PlotAntennaLayout([ws, parfile])	Description:
PlotDirectionTriangles([ws, parfile])	Description:

A number of tools useful in calibrating radio data

Module author: Heino Falcke <h.falcke@astro.ru.nl>

class pycrtools.tasks.pulsecal.DirectionFitTriangles(ws=None, parfile=None, **kwargs)

Find the direction of a source provided one has the measured delay of arrival and the positions of the antenna.

Description:

This task uses the function hDirectionTriangulationsCartesian() to calculate a list of arrival directions in Cartesian coordinates of a pulse/source from all possible triangles of (groups of three) antennas and the measured arrival times at these antennas.

For the direction finding it is assumed that the signal arrives as a plane wave. If one triangle of antennas does not give a valid solution a solution at the horizion is returned with the complex part of the solution (the “closure error”) returned in Task.error.

To cope with near-field sources for each triangle the coordinates of its center are also calculated. This allows one to later look for points where the dircetions from all triangles intercept.

The inverse of the average lengths of the triangle baselines are returned in weights giving some indication how accurate the measurement in principle can be.

From three antennas we get in general two solutions for the direction, unless the arrival times are out of bounds, i.e. larger than the light-time between two antennas. Usually, when the three antennas are in a more or less horizontal plane, one of the solutions will appear to come from below the horizon (el < 0) and can be discarded. With sign_of_solution one can pick either the positive of the negative elevation.

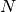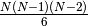If triangles are provided then the Directions, Origins, and weights vectors have results (times number of components of each result, i.e. times three for origins and times one for the rest.)

The actually measured lag is assumed to consist of two parts: the geometric delay due to light travel times plus the cable delay in each antenna.

measured timelag = expected geometric delay + cable delay + residual delay

What we do in the iteration is to use the above equation in the form

measured timelag - (cable delay + residual delay + delta delays[i]) - expected geometric delay = 0

with a delta delay that is determined at each step and then subsumed into the residual delay.

Output:

The main result will be in Task.meandirection which contains the direction vector to the source in Cartesian coordinates. See also Task.meandirection_azel and Task.meandirection_azel_deg.

The array Task.delays will contain the final cable delays needed to get a coherent signal for the final position. The delays as a function of iteration are in Task.delays_history[iteration]

Coordinate Systems

• Azimuth/Elevation is defined as North (0 degrees) through East (90 degrees) for Az and El running from 90 degree at the zenith to 0 degree at the horizon
• For spherical coordindates Az/phi is defined as East (0 degree) through North (90 degree) and theta running from 0 degree at the zenith to 90 degree at the horizon

See also:

CrossCorrelateAntennas, LocatePulseTrain, FitMaxima

Example:

file=open("$LOFARSOFT/data/lofar/oneshot_level4_CS017_19okt_no-9.h5")
file["ANTENNA_SET"]="LBA_OUTER"
file["BLOCKSIZE"]=2**17

file["SELECTED_DIPOLES"]=["017000001","017000002","017000005","017000007","017001009","017001010","017001012","017001015","017002017","017002019","017002020","017002023","017003025","017003026","017003029","017003031","017004033","017004035","017004037","017004039","017005041","017005043","017005045","017005047","017006049","017006051","017006053","017006055","017007057","017007059","017007061","017007063","017008065","017008066","017008069","017008071","017009073","017009075","017009077","017009079","017010081","017010083","017010085","017010087","017011089","017011091","017011093","017011095"]

timeseries_data=file["TIMESERIES_DATA"]
positions=file["ANTENNA_POSITIONS"]

# First determine where the pulse is in a simple incoherent sum of all time series data

pulse=trun("LocatePulseTrain",timeseries_data,nsigma=7,maxgap=3)

# Normalize the data which was cut around the main pulse
pulse.timeseries_data_cut[...]-=pulse.timeseries_data_cut[...].mean()
pulse.timeseries_data_cut[...]/=pulse.timeseries_data_cut[...].stddev(0)

# Cross correlate all pulses with each other
crosscorr=trun('CrossCorrelateAntennas',pulse.timeseries_data_cut,oversamplefactor=5)

# And determine the relative offsets between them
mx=trun('FitMaxima',crosscorr.crosscorr_data,doplot=True,refant=0,plotstart=4,plotend=5,sampleinterval=10**-9,peak_width=6,splineorder=2)

# Now fit the direction and iterate over cable delays to get a stable solution
direction=trun("DirectionFitTriangles",positions=positions,timelags=hArray(mx.lags),maxiter=10,verbose=True,doplot=True)

print "========================================================================"
print "Fit Arthur Az/El   ->  143.409 deg 81.7932 deg"
print "Triangle Fit Az/EL -> ", direction.meandirection_azel_deg,"deg"

# Triangle Fit Az/EL ->  (144.1118392216996, 81.84042919170588) deg for odd antennas
# Triangle Fit Az/EL ->  (145.17844721833896, 81.973693266380721) deg for even antennas

Input parameters

NAnt

Number of antennas and time lags. If set explicitly, take only the first NAnt antennas from Task.positions and Task.timelags.

NTriangles

Number of Triangles = NAnt*(NAnt-1)*(NAnt-2)/6.

cabledelays

Know (fixed) cable delays that one needs to correct measured delays for.

centers

Cartesian coordinates of center for each triangle.

delay_error [default value: 1e-12 ]

Target for the RMS of the delta delays where iteration can stop.

delayindex

Index array of good delays.

delays_history

Instrumental delays for each iteration (for plotting)

delays_historyT

Instrumental delays for each iteration (for plotting)

delta_delays

Additional instrumental delays needed to calibrate array will be added to timelags and will be updated during iteration

direction_guess [default value: False ]

If a tuple of two numbers (azimut, elevation) then this is an initial guess for the direction (currently only for plotting).

direction_guess_label [default value: “direction guess” ]

A label for plotting indicating where the direction guess was coming from.

directions

Cartesian direction vector for each triangle

doplot [default value: False ]

Plot results.

error_tolerance [default value: 1e-10 ]

Level above which a closure error is considered to be non-zero (take -1 to ignore closure errors).

errors

Closure errors for each triangle (nor error if = 0).

expected_timelags

Exact time lags expected for each antenna for a given source position

goodones

Scratch array to hold good directions.

index

Index array of good triangles.

max_delay [default value: 1.5e-08 ]

Maximum allowed delay. If a delay for an antenna is larger than this it will be flagged and igrnored

maxiter [default value: 1 ]

if >1 iterate (maximally tat many times) position and delays until solution converges.

meandirection_azel

Mean direction as Azimuth (N->E), Elevation tuple.

meandirection_azel_deg

Mean direction as Azimuth (N->E), Elevation tuple in degrees.

meandirection_spherical

Mean direction in spherical coordinates.

measured_geometric_timelags

Time lags minus cable delay = pure geometric delay if no error

minrmsfactor [default value: 1.0 ]

Minimum rmsfactor (see rmsfactor) for selecting bad antennas.

plot_finish

Function to be called after each plot to determine whether to pause or not (see plotfinish())

plot_name [default value: “” ]

Extra name to be added to plot filename.

plotant_end

Last antenna to plot plus one.

plotant_start [default value: 0 ]

First antenna to plot.

positions

hArray with Cartesian coordinates of the antenna positions

refant [default value: 0 ]

Reference antenna for which geometric delay is zero.

residual_delays

Residual delays needed to calibrate the array after correction for known cable delays. Will be subtracted from the measured lags (correced for cable delays) or added to the expected. The array will be updated during iteration

rmsfactor [default value: 3.0 ]

How many sigma (times RMS) above the average can a delay deviate from the mean before it is considered bad (will be reduced with every iteration until minrsmfactor).

solution [default value: 1 ]

Can be +/-1, determine whether to take the upper or the lower (‘into the ground’) solution.

timelags

hArray with the measured time lags for each event and each antenna

total_delays

Total instrumental (residual+cable) delays needed to calibrate the array. Will be subtracted from the measured lags or added to the expected. The array will be updated during iteration

triangles_size

Average size for each triangle.

unitname [default value: “ns” ]

Unit corresponding to scale factor.

unitscalefactor [default value: 1e-09 ]

Scale factor to apply for printing and plotting.

verbose [default value: False ]

Print progress information.

Output parameters

delta_delays_mean_history [default value: [] ]

Mean of the difference between expected and currently calibrated measured delays for each iteration

delta_delays_rms_history [default value: [] ]

RMS of the difference between expected and currently calibrated measured delays for each iteration

good_antennas

List of integer indices pointing to the good antennas in the original list

good_positions

hArray with Cartesian coordinates of the antenna positions for good antennas

good_timelags

hArray the measured time lags for each event and all good antennas

meancenter

Cartesian coordinates of mean central position of all good triangles

meandirection

Cartesian coordinates of mean direction from all good triangles

n_good_antennas

Number of good antenna time lags

n_timelags

Number of time lags provided

ngood [default value: 0 ]

Number of good triangles (i.e., without closure errors)

ngooddelays [default value: 0 ]

Number of good delays (i.e., with only minor deviation)

class pycrtools.tasks.pulsecal.FitMaxima(ws=None, parfile=None, **kwargs)

Find the maxima in multiple datsets and fit a basis spline polynomial to the data around their respective maximum. Then determine where the maximum in the interpolated data will be. This allows one to determine the maximum with subsample precision.

Usage:

Task = FitMaxima()(data[n_datasets,n_samples], peak_width=20, nsubsamples=16, ncoeffs=5, splineorder=3, doplot=False, plotend=4, plotstart=0, sampleinterval=None, refant=None) -> Task.maxx, Task.maxy, Task.lag

The main result will be in Task.maxx which returns the (fractional) sample number of the maximum and Task.maxy the y-value of the maximum. Task.lag returns the relative offset of the peaks relative to the reference dataset (refant) in user units, specified by sampleinterval.

See also:

CrossCorrelateAntennas, LocatePulseTrain

Example:

file=open("/Users/falcke/LOFAR/usg/data/lofar/oneshot_level4_CS017_19okt_no-9.h5")
file["BLOCKSIZE"]=2**int(round(math.log(file["DATA_LENGTH"][0],2)))
file["SELECTED_DIPOLES"]=[f for f in file["DIPOLE_NAMES"] if int(f)%2==1] # select uneven antenna IDs
timeseries_data=file["TIMESERIES_DATA"]
(start,end)=trun("LocatePulseTrain",rf.TimeBeamIncoherent(timeseries_data),nsigma=7,maxgap=3)
start-=16
end=start+int(2**math.ceil(math.log(end-start,2)));
timeseries_data_cut=hArray(float,[timeseries_data.shape()[-2],end-start])
timeseries_data_cut[...].copy(timeseries_data[...,start:end])
timeseries_data_cut[...]-=timeseries_data_cut[...].mean()
timeseries_data_cut[...]/=timeseries_data_cut[...].stddev(0)
crosscorr_data=tasks.pulsecal.CrossCorrelateAntennas()(timeseries_data_cut).crosscorr_data
crosscorr_data.abs()
crosscorr_data[...].runningaverage(15,hWEIGHTS.GAUSSIAN)

mx=trun("FitMaxima",crosscorr_data,doplot=True,refant=0,sampleinterval=5)

print "Lags =",list(mx.lags),"nanoseconds."

Input parameters

covariance

dim2

doplot [default value: False ]

Plot results.

fits_xdata

fits_ydata

legend [default value: None ]

List containing labels for each antenna data set for plotting the label

ncoeffs

Number of breakpoints to fit spline polynomial around the peak.

newfigure [default value: True ]

Create a new figure for plotting for each new instance of the task.

nsubsamples [default value: 16 ]

Divide each original sample into that many finer pixels. Determines maximum resolution of fit.

peak_width [default value: 20 ]

Width of the data over which to fit the peak.

plotend [default value: 4 ]

Stop plotting at this data set.

plotstart [default value: 0 ]

Start plotting at this data set.

refant [default value: None ]

Reference antenna who’s maximum determines the zero point of the x-axis (e.g., to get relative delays).

sampleinterval [default value: None ]

Separation of two subsequent samples on the x-axis in desired units - used to return lags in proper units.

splineorder [default value: 3 ]

Order of spline to fit. 3=cubic spline.

xdata

x-axis value for the fit

xpowers

xvalues

Samplenumber for the time series data

Output parameters

coeffs

Coefficients of spline fit.

figure [default value: None ]

The matplotlib figure containing the plot

lags [default value: None ]

X-values of fitted maxima

maxx [default value: None ]

X-values of fitted maxima

maxy [default value: None ]

Y-values of fitted maxima

class pycrtools.tasks.pulsecal.LocatePulseTrain(ws=None, parfile=None, **kwargs)

Usage

LocatePulseTrain()(timeseries_data[nantennas,blocklen],timeseries_data_sum[blocklen]=None,nsigma=7,maxgap=7,minpulselen=7) -> Task.start, Task.end, Task.time_series_cut

Description

Finds the pulse train with the highest peak in time series data, determine its location, and cut out the time series data around the pulse. If the input array has multiple dimensions (multiple antennnas are present), then sum the antennas first and search the pulse in the sum of all antennas or look for the mean pulse location for all antennas.

The task calculates noise and threshold level above which to find pulse trains. A pulse train can have gaps of some N=maxgaps samples which are below the threshold and yet are considered part of the pulse train (i.e., this is the maximum separation of individual pulses to be considered part of the pulse train.).

With the parameter search_window the search can be limited to the range of samples between those two numbers.

If the parameter timeseries_data_sum is provided (a 1D array with a time series, e.g. an incoherent beam of all antennas) then the peak will be searched in that time series and not recalculated.

If search_per_antenna=True then the peaks are searched in each antenna. From all antennas where a peak was found the median peak location and length is taken.

Results:

Returns start and end index of the strongest pulse in Task.start and Task.end. The cut-out time series is returned in Task.timeseries_data_cut.

The summed time series from all data sets (if a 2D array was provided) is returned in Task.timeseries_data_sum

For search_per_antenna=True the list Task.peaks_found_list contains the indices of all antennas where a peak was found. The number of antennas with peaks is self.npeaks_found. Start and end of the pulses for each antenna with peak are found are in self.maxsequences. The smallest and largest start location of all antennas can be found in Task.start_min, Task.start_max. See also Task.lengths_min, Task.lengths_max, and Task.lengths_median for information on the width of these peaks.

See hFindSequenceGreaterThan() for a description of the other parameters.

See also:

hFindSequenceGreaterThan()

Example

file=open("/Users/falcke/LOFAR/usg/data/lofar/oneshot_level4_CS017_19okt_no-9.h5") #
file["BLOCKSIZE"]=2**int(round(math.log(file["DATA_LENGTH"][0],2)))
file["SELECTED_DIPOLES"]=["017000001", "017000002", "017000005", "017000007", "017001009", "017001010", "017001012", "017001015", "017002017", "017002019", "017002020", "017002023", "017003025", "017003026", "017003029", "017003031", "017004033", "017004035", "017004037", "017004039", "017005041", "017005043", "017005045", "017005047", "017006049", "017006051", "017006053", "017006055", "017007057", "017007059", "017007061", "017007063", "017008065", "017008066", "017008069", "017008071", "017009073", "017009075", "017009077", "017009079", "017010081", "017010083", "017010085", "017010087", "017011089", "017011091", "017011093", "017011095"]
pulse=trun('LocatePulseTrain',file["TIMESERIES_DATA"])
#(pulse.start,pulse.end) -> (65806L, 65934L)
pulse.timeseries_data_sum.plot(highlight=(pulse.start,pulse.end),nhighlight=1)
pulse.timeseries_data_cut[0].plot()

Input parameters

cut_to_power_of_two [default value: True ]

Cut the time series to a length which is a power of two?

docut [default value: True ]

Cut the time series around the pulse and return it in timeseries_data_cut.

doplot [default value: False ]

Produce output plots.

maxgap [default value: 7 ]

Maximum gap length allowed in a pulse where data is not above the threshold

maxlen [default value: 1024 ]

Maximum length allowed for the pulse train to be returned.

maxnpeaks [default value: 256 ]

Naximum number of train peaks to look for in data

minlen [default value: 32 ]

Minimum length allowed for cutting the time time series data.

minpulselen [default value: 7 ]

Minimum width of pulse.

nantennas

Number of antennas in data file.

nblocks [default value: 16 ]

The time series data is subdivided in nblock blocks where the one with the lowest RMS is used to determine the threshold level for finding peaks.

nsigma [default value: 7 ]

Pulse has to be nsigma above the noise.

plot_filename [default value: “” ]

Base filename to store plot in.

plot_finish

Function to be called after each plot to determine whether to pause or not (see ::func::plotfinish)

plot_name [default value: “” ]

Extra name to be added to plot filename.

prepulselen [default value: 16 ]

Safety margin to add before the start of the pulse for cutting and start.

search_per_antenna [default value: False ]

Search pulses per antennas and then return the average of all peaks found.

search_window [default value: False ]

False - if set to a tuple with two integer indices (start, end), pointing to locations in the array, only the strongest peak between those two locations are being considered. Use -1 for start=0 or end=len(array).

timeseries_data_sum [default value: None ]

Incoherent (squared) sum of all antennas.

timeseries_length

Length of the full input time series.

Output parameters

cutlen [default value: None ]

Length of the cut-out data.

end [default value: 32 ]

End index of the strongest pulse train

indexlist

Original locations of the peaks found in the data

maxima [default value: None ]

Values of the maxima of the pulse trains

npeaks [default value: 0 ]

Number of peaks found in data

start [default value: 0 ]

Start index of the strongest pulse train

timeseries_data_cut

Contains the time series data cut out around the pulse.

class pycrtools.tasks.pulsecal.PlotAntennaLayout(ws=None, parfile=None, **kwargs)

Description:

Plot the layout of the current dataset on the ground.

Usage:

See also: DirectionFitTriangles

Example:

file=open("$LOFARSOFT/data/lofar/oneshot_level4_CS017_19okt_no-9.h5")
file["ANTENNA_SET"]="LBA_OUTER"
file["SELECTED_DIPOLES"]="odd"
positions=file["ANTENNA_POSITIONS"]
layout=trun("PlotAntennaLayout",positions=positions,sizes=range(48),names=range(48))

Input parameters

colors [default value: “b” ]

hArray of dimension [NAnt] with the values for the colors of the plot

names [default value: False ]

hArray of dimension [NAnt] with the names or IDs of the antennas

newfigure [default value: True ]

Create a new figure for plotting for each new instance of the task.

normalize_colors [default value: True ]

Normalize the colors to run from 0-1.

normalize_sizes [default value: True ]

Normalize the sizes to run from 0-1.

plot_clf [default value: True ]

Clean window before plotting?

plot_finish

Function to be called after each plot to determine whether to pause or not (see ::func::plotfinish)

plot_name [default value: “” ]

Extra name to be added to plot filename.

plotlegend [default value: False ]

Plot a legend

positions

hArray of dimension [NAnt,3] with Cartesian coordinates of the antenna positions (x0,y0,z0,...)

positionsT

hArray with transposed Cartesian coordinates of the antenna positions (x0,x1,...,y0,y1...,z0,z1,....)

size [default value: 300 ]

Size of largest point.

sizes [default value: 20 ]

hArray of dimension [NAnt] with the values for the size of the plot

sizes_max [default value: None ]

If set, then use this as the maximum scale for the sizes, when normalizing.

sizes_min [default value: None ]

If set, then use this as the minimum scale for the sizes, when normalizing.

title [default value: False ]

Title for the plot (e.g., event or filename)

Output parameters

NAnt

Number of antennas.

class pycrtools.tasks.pulsecal.PlotDirectionTriangles(ws=None, parfile=None, **kwargs)

Description:

Plot the directions towards a source found by triangle fitting. This will average directions from triangles of antennas with the same center into one mean direction and then plot a mean direction arrow, for this subarray.

This will als plot the underlying layout of antennas.

Usage:

See also: DirectionFitTriangles

Example:

filename="oneshot_level4_CS017_19okt_no-9.h5"
file=open("$LOFARSOFT/data/lofar/"+filename)
file["ANTENNA_SET"]="LBA_OUTER"
file["BLOCKSIZE"]=2**17

file["SELECTED_DIPOLES"]=["017000001","017000002","017000005","017000007","017001009","017001010","017001012","017001015","017002017","017002019","017002020","017002023","017003025","017003026","017003029","017003031","017004033","017004035","017004037","017004039","017005041","017005043","017005045","017005047","017006049","017006051","017006053","017006055","017007057","017007059","017007061","017007063","017008065","017008066","017008069","017008071","017009073","017009075","017009077","017009079","017010081","017010083","017010085","017010087","017011089","017011091","017011093","017011095"]

timeseries_data=file["TIMESERIES_DATA"]
positions=file["ANTENNA_POSITIONS"]

# First determine where the pulse is in a simple incoherent sum of all time series data

pulse=trun("LocatePulseTrain",timeseries_data,nsigma=7,maxgap=3)

# Normalize the data which was cut around the main pulse for correlation
pulse.timeseries_data_cut[...]-=pulse.timeseries_data_cut[...].mean()
pulse.timeseries_data_cut[...]/=pulse.timeseries_data_cut[...].stddev(0)

# Cross correlate all pulses with each other
crosscorr=trun('CrossCorrelateAntennas',pulse.timeseries_data_cut,oversamplefactor=5)

# And determine the relative offsets between them
mx=trun('FitMaxima',crosscorr.crosscorr_data,doplot=True,refant=0,plotstart=4,plotend=5,sampleinterval=10**-9,peak_width=6,splineorder=2)

# Now fit the direction and iterate over cable delays to get a stable solution
direction=trun("DirectionFitTriangles",positions=positions,timelags=hArray(mx.lags),maxiter=10,verbose=True,doplot=True)

print "========================================================================"
print "Fit Arthur Az/El   ->  143.409 deg 81.7932 deg"
print "Triangle Fit Az/EL -> ", direction.meandirection_azel_deg,"deg"

# Triangle Fit Az/EL ->  (144.1118392216996, 81.84042919170588) deg for odd antennas
# Triangle Fit Az/EL ->  (145.17844721833896, 81.973693266380721) deg for even antennas

p=trun("PlotDirectionTriangles",centers=direction.centers,positions=direction.positions,directions=direction.directions,title=filename)

Input parameters

NSubArrays

Number of subarrays for which to average the direction from triangles

SubArrayFactor

Factor used to determine the number of subarrays for which to average the direction from triangles NSubArrays=NAnt*SubArrayFactor

centers

hArray of dimension [NTriangles,3] with Cartesian coordinates of the centers of each triangle (x0,y0,z0,...)

direction_arrow_length [default value: 10.0 ]

Relative length of the direction arrows relative to the maximum size of the array

directions

hArray of dimension [NTriangles,3] with Cartesian coordinates of the direction each triangle has given (x0,y0,z0,...)

newfigure [default value: True ]

Create a new figure for plotting for each new instance of the task.

plotlegend [default value: False ]

Plot a legend

positions

hArray of dimension [NAnt,3] with Cartesian coordinates of the antenna positions (x0,y0,z0,...)

positionsT

hArray with transposed Cartesian coordinates of the antenna positions (x0, x1,..., y0, y1,..., z0, z1,....)

title [default value: False ]

Title for the plot (e.g., event or filename)

Output parameters

NAnt

Number of antennas.

NTriangles

Number of Triangles = NAnt*(NAnt-1)*(NAnt-2)/6 = length of directions.