Goal
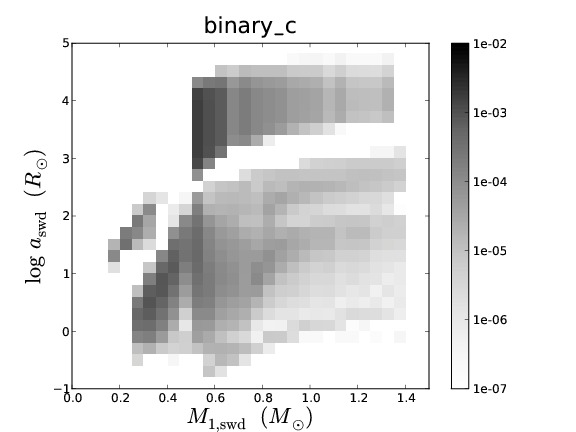
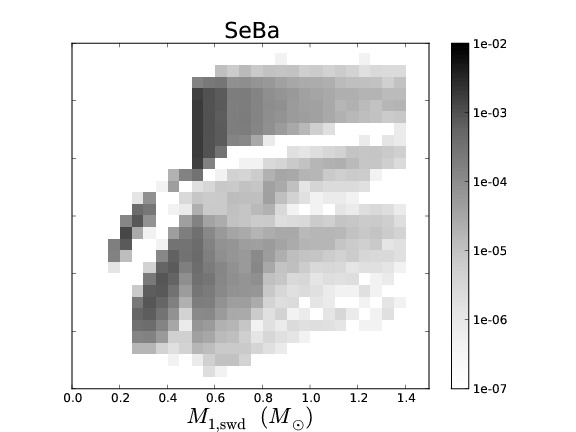
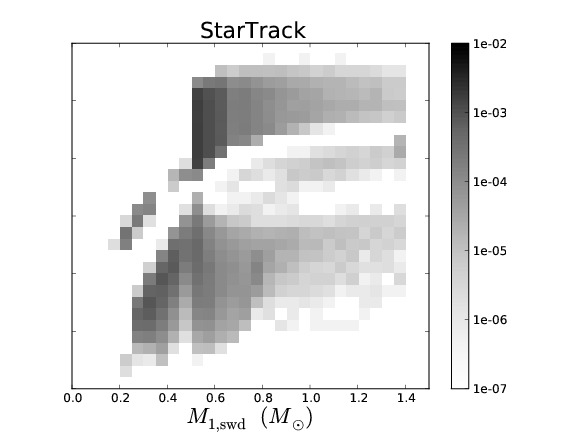
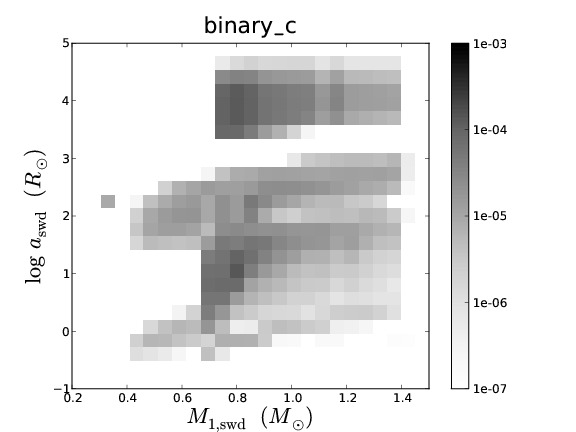
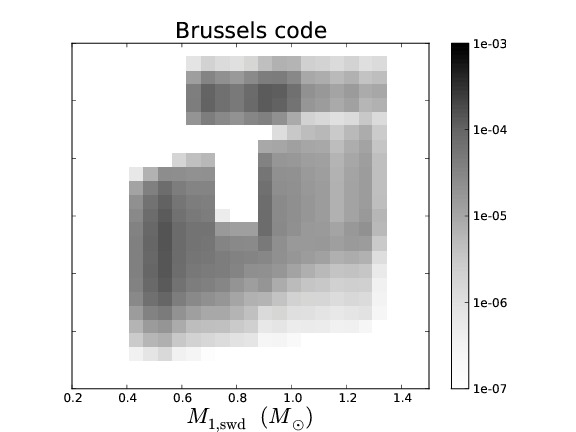
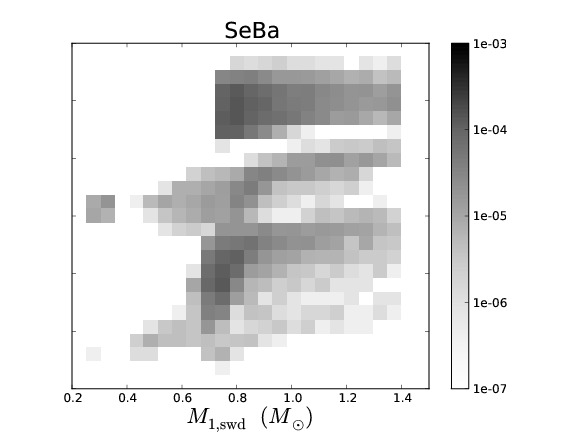
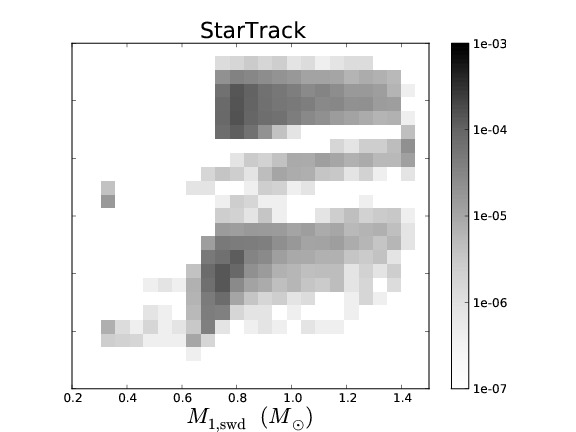
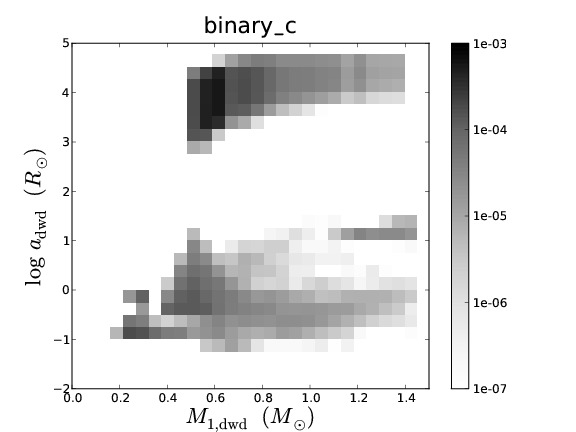
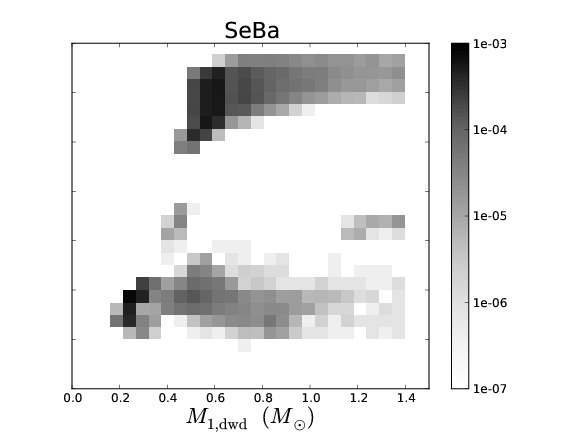
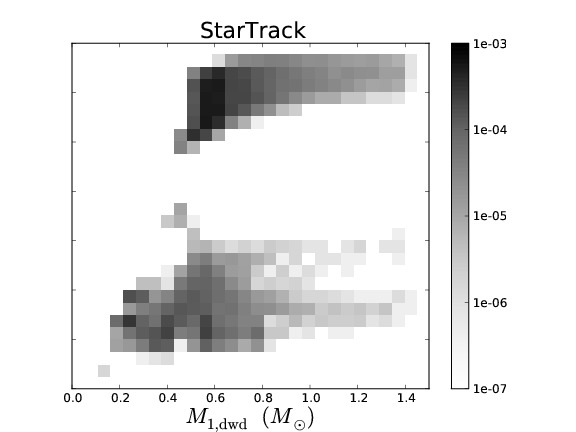
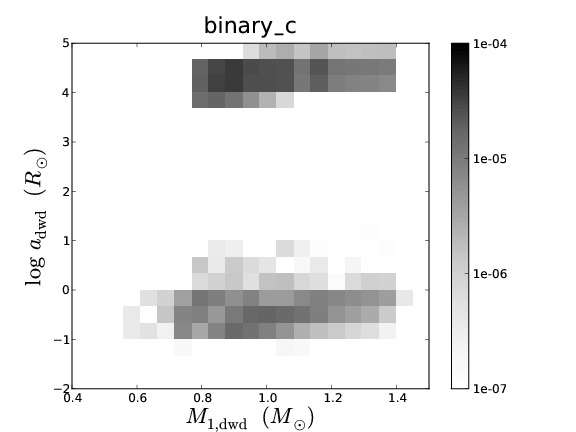
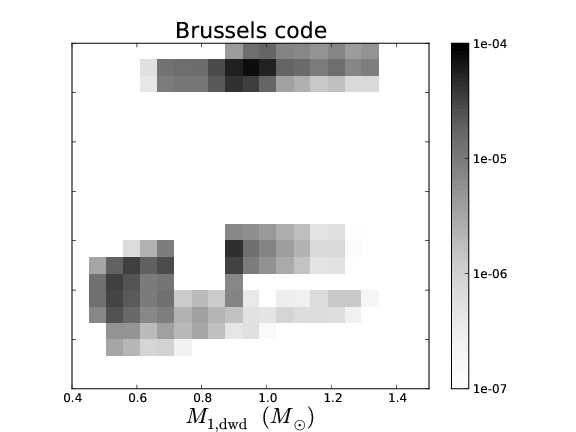
Binary population synthesis (BPS) modelling is a very effective tool to study the evolution and properties of various types of close binary systems. The uncertainty in the parameters of the model and their effect on a population can be tested in a statistical way, which then leads to a deeper understanding of the underlying (sometimes poorly understood) physical processes involved. Several BPS codes exist that have been developed with different philosophies and aims. Although BPS has been very successful for studies of many populations of binary stars, in the particular case of the study of the progenitors of supernovae Type Ia, the predicted rates and ZAMS progenitors vary substantially between different BPS codes.
To understand the predictive power of BPS codes, we study the similarities and differences in the predictions of four different BPS codes for low- and intermediate-mass binaries. To simplify the complex problem of comparing BPS codes, we equalise the input assumptions as much as possible. We discuss the similarities and differences in the predicted populations of the different BPS codes. We examine the causes for the differences that remain and in particular whether they are caused by assumptions (that can not be equalized between the codes) or by numerical effects, e.g. a lack of accuracy in BPS codes.